lysoli.blogg.se

1. #Max drawdown geekforgeek how to
2. #Max drawdown geekforgeek full
3. #Max drawdown geekforgeek code
4. #Max drawdown geekforgeek series

Test10 - running drawdown test with 500 period rolling window. Test9 - running drawdown test with 360 period rolling window. Test8 - running drawdown test with 180 period rolling window. Test7 - running drawdown test with 60 period rolling window. Here we compare to the results generated from my efficient rolling window algorithm where only the latest observation is added and then it does it's magic test6 - running drawdown test with 30 period rolling window. Test5 - simple drawdown test with 500 period rolling window. Test4 - simple drawdown test with 360 period rolling window. Test3 - simple drawdown test with 180 period rolling window. Test2 - simple drawdown test with 60 period rolling window.

#Max drawdown geekforgeek full

Here we take a simple drawdown implementation and re-calculate for the full window each time test1 - simple drawdown test with 30 period rolling window. I want to share this as the effort required to replicate this work is quite high. I have gone ahead and written a solution to this in C#. Return mddd_start, mddd_end, mddd_durationĮxample usage: # compute cumulative returnsĭfc = pd.This is quite a complex problem if you want to solve this in a computationally efficient way for a rolling window. Min_idx = dfw) & (dfw.index mddd_duration: # find the index of the data point that is minimum this is an argmin # label only the negative part of the underwater NDD stands for negative-side drawdown. 5%ĭictionary containing the start, end dates and duration in months for the maximumĭfw.loc = i.left) & (dfw.index = -threshold else x, min_per_int))))

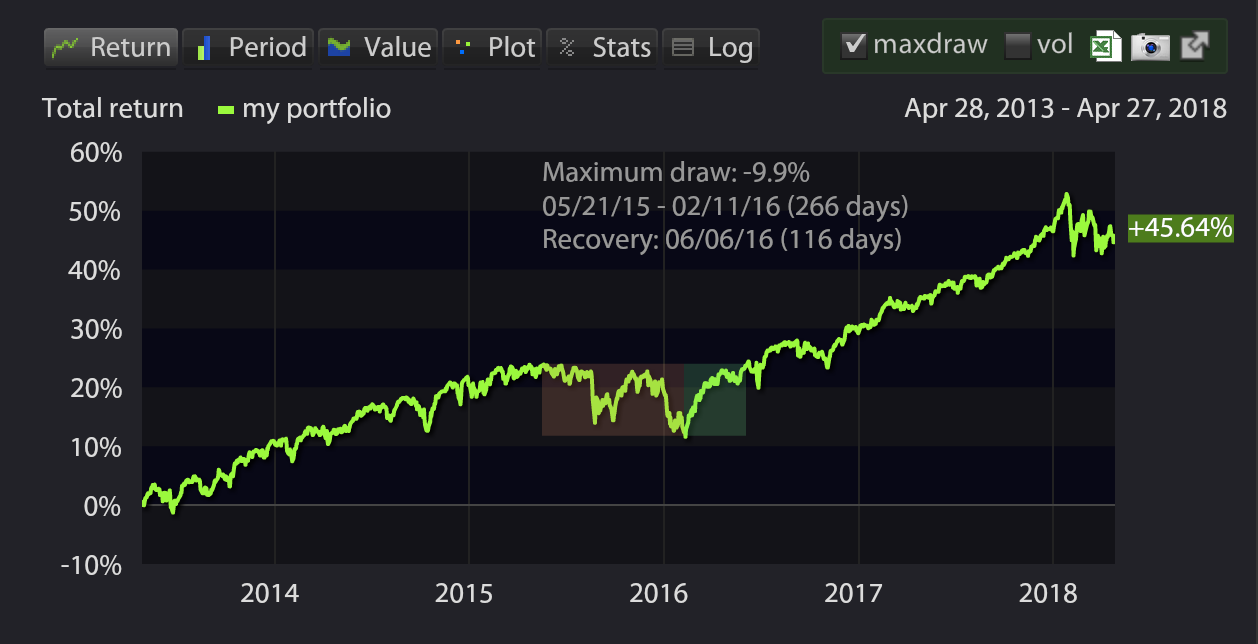
Threshold (float): only look at drawdowns greater than this in absolute value e.g. Labels all drawdowns larger in absolute value than a threshold and returns theĭrawdown of maximum duration (not the max drawdown necessarily but most often theyĭfw (pd.DataFrame): monthly data, the pre-computed drawdowns or underwater. def max_dur_drawdown(dfw, threshold=0.05): The solution can be easily adapted to find the duration of the maximum drawdown. This solution is tested and works but here I'm computing the maximum duration drawdown and NOT the duration of the maximum drawdown. It could be better to add: xs -= (np.min(xs) - 10) Print(f"solution 1: peak \n rate :įurther the price of an asset cannot be negative so xs = np.random.randn(n).cumsum() Label="mdd 2", color='Green', markersize=10) Label="mdd 1", color='Red', markersize=10) Pos_peak2 = np.argmax(xs) # start of period Xs)/np.maximum.accumulate(xs)) # end of the period Pos_min2 = np.argmax((np.maximum.accumulate(xs). Pos_peak1 = np.argmax(xs) # start of period Pos_min1 = np.argmax(np.maximum.accumulate(xs) - xs) # end of the period ( np.maximum.accumulate(xs) - xs ) / np.maximum.accumulate(xs)Ī short example for prooving that formula given by behzad.nouri can produce wrong result. You just need to divide this drop in nominal value by the maximum accumulated amount to get the relative ( % ) drawdown. I = np.argmax(np.maximum.accumulate(xs) - xs) # end of the period

#Max drawdown geekforgeek code

Related code (from behzad.nouri) below: n = 1000 Recent Corona Virus crisis, drop 33.9%, 1,1148.75 pointsīy applying this method to period after 2000, you'll see Corona Virus Crisis rather than 2007-08 Financial Crisis.

#Max drawdown geekforgeek series

For example, if you would apply this to time series that is ascending over the long run (for example stock market index S&P 500), the most recent drop in value (higher nominal value drops) will be prioritized over the older decrease in value as long as the drop in nominal value/points is higher. What you end up having is the maximum drop in the nominal value rather than a relative drop in value (percentage drop). S = S0*np.exp(X) # geometric brownian motion #īehzad.nouri solution is very clean, but it's not a maximum drawdow (couldn't comment as I just opened my account and I don't have enough reputation atm). W = np.cumsum(W)*np.sqrt(dt) # standard brownian motion #

# create random walk which I want to calculate maximum drawdown for:

#Max drawdown geekforgeek how to

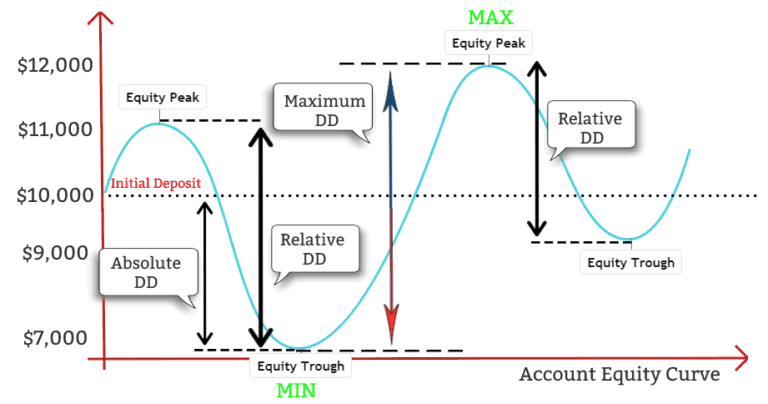
If anyone knows how to identify the places where the drawdown begins and ends, I'd really appreciate it! import pandas as pd So far I've got code to generate a random time series, and I've got code to calculate the max drawdown. I want to mark the beginning and end of the drawdown on a plot of the timeseries like this: Given a time series, I want to calculate the maximum drawdown, and I also want to locate the beginning and end points of the maximum drawdown so I can calculate the duration.